國中理化就是死背公式?
這我倒不這麼認為,死背公式,小考可能有用,但是到模擬考或大考,很大機會完蛋 !為什麼?因為大考範圍大,題目都是混合著兩三個觀念於一題,你如果是以死背公式的方式來學習理化,到大考的表現一定會變差!
但我的意思並不是說公式都不用背,而是「理解後再把它記起來」,我舉個例子,密度,在準備把「密度 = 質量 / 體積」背起來之前,先把它的的意義理解,密度的意義是:「我這個物體每一單位體積它所佔的質量是多少」,先理解了這個定義,背這個公式才有意義!
多做題目有幫助嗎?
多做題目非常棒!但請把大部分的時間花在「會考題」上!因為,它的名字就告訴你了,它就叫”會考”題,而且它是由全國的命題老師達成共識後,所出出來的題目,表示什麼?表示命題老師們希望你們升高中前,對於理化,必須要知道的理化知識,所以請優先把時間花在歷屆會考題上,有閒暇的時機,再去做其他較刁鑽的題目。畢竟,很現實的,「會考的分數」,才是有意義的分數,對吧!
而關於會考題,可以拉到15年 ~ 20年前的會考題來練習,「以前的會考題著重計算,現在的會考題著重觀念」,兩者互補,把每一題的每一個選項都搞懂,知道它為什麼對,為什麼錯,是我認為最重要的練習方式,其它坊間的題目,有時間再來做練習吧!
做題目時會感到混亂且不知如何下手是正常的嗎?
這是很正常的喔,有幾個原因:
◆ 如果你是剛升上國二的學生,這是你第一次接觸到科目,它不像數學,是從國小一路學上來的,所以沒有「熟悉感」,再來理化這是一個又要計算,又要背,又要理解的科目,所以如果是一開始接觸到的學生,遇到理化題目會慌亂且不知如何下手是正常的喔!
◆ 若你學習了一段時間後,發現還是有這個現象的話,那問題有可能在於學習的方式,幾個較大的原因:
1. 你看不太懂題目要問什麼。這個部分的話簡單,靜下心來,先不用著急著要解出答案,先不管答案,好好的「欣賞一下」題目,多練習會考題或素養題,這個問題就能慢
2. 基本的觀念沒搞懂,或者是公式的定義沒搞的很懂,這個最常見!
3. 還有一個非戰之罪,因為國中很多觀念沒辦法說得很清楚,都點到而已,要到高中才會學的透徹。但題目有時候不小心出的超過範圍,才會有這個不知如何下手的情況!
補習班對於理化這科是個好的選擇嗎?
因為我之前有去過學區補習班上班過,而這也是我為什麼投入線上教學的原因😂 ~ ~
就我看到補習班的實況:
1. 學生在下課後來補習,感覺得出來他們非常疲累,就算小班制會管打瞌睡,但感覺精神都放在把眼皮撐開 ~ ~
2. 補習班派的功課趁著扒飯的時候亂猜一通,題目本上有字就好,這基本上也失去了補習班加強學習的意義!
3. 補習班的班導師真的是本科系的嗎?這點也是家長需要去考慮的,畢竟,學生的課業問題若不能即時解決,慢慢累積後,對於學習會築起一道障礙,讓學生放棄治療!
所以,如果是我,我會覺得補習是一件不划算的事。現在網路發達,滿多線上教學的,好好地去選擇老師,應該能做到省時省錢的效果!
讀好理化的方法
「內容理解很重要,自問自答很重要」
理化的內容理解對於解題來說是很重要的,先多花一點時間在內容理解上,等到結打開了,做起題目就會有相當的信心及成就感 !
那如何做到「好」的理解,而不是自以為理解的理解 ?「為什麼」這三個字很重要,例如以數學來舉例,「三角形的內角合為180o」,這個是課本上提供給你的內容,但這時候你就要問自己,為什麼?
因為正方形切成一半,就變成兩個等腰直角三角形,所以三角形的內角合的等於 180o
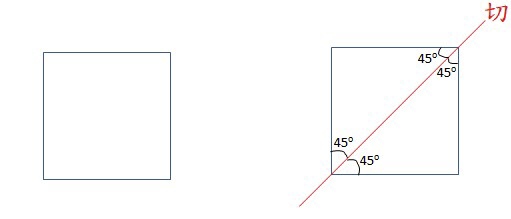
但這還不夠,你還要繼續往下問,那如果不是等腰直角三角形呢?一樣,因為四邊形的內角合等於 360o,所以 a+b+c 等於 180o

還不夠,還有最後一個問題,正方形內角合等於 360o,那平行四邊形的內角合也等於 360o 嗎?
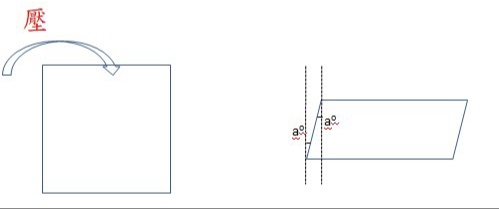
是的,先看平行四邊形的左半邊,因為左邊上面的直角經過擠壓後變成(90+a)o,而左邊下方的直角則變成 (90-a)o,所以兩者相加跟原來一樣還是 180o,那右邊跟左邊就是一樣的理解模式,所以平行四邊形內角合等於 360o,跟正方形或長方形一樣!
所以,請不斷問自己為什麼?理化講義上這句話的敘述到底什麼意思,這樣你才有辦法完全理解吸收,而不是一知半解 !
除了自問自答外,也可假裝有人要被你教,你要怎麼去解釋這個觀念或這個題目,這也可以加強你對內容的理解跟吸收!
儘可能嘗試著自己做每個理化章節的重點整理,可以使用心智圖或樹狀圖(如下圖),多花一點時間在這種地方!
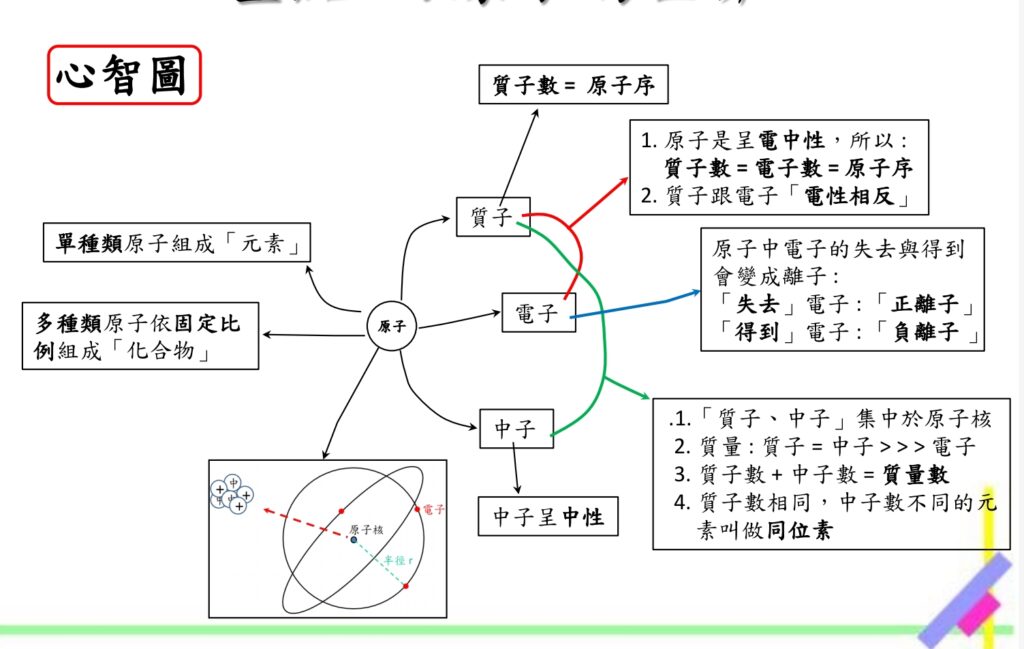
「會考題練習跟問題的提出很重要」
題目練習就專注於會考題,由於會考題每個章節的題目數不多(我已經幫你們整理在我的講解視頻啦),所以要注意練習的時間間隔,每次練習的時間最好隔一個月至兩個月之間,才不會造成有記憶效應(就是以為自己理解,但其實是因為背起來的關係,而不是理解)!
而當有問題時,請立刻提出,避免問題的累積而造成往後章節的學習不連貫,這很容易變成惡性循環而放棄治療啊!
大概就是這樣,有想到什麼再來補充😆
有理化問題歡迎寄信給我
